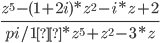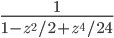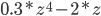On m'a demandé récemment à plusieurs reprises de me dire comment est arrivé reflex4you.com, et quels ont été les défis. Alors j'ai décidé d'écrire un article à ce sujet. Cet article. Votre article. Sans soldes. L'idée de représenter les fonctions complexes, comme toute idée géniale qui se respecte, est née d'une frustration en Terminale S. Alors que j'apprenais avec curiosité comment un nombre 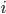mis au carré pouvait faire -1, je me suis demandé s'il n'y avait pas une manière visuelle de voir les choses. En effet, quand on calculait des carrés comme 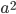, on imaginait un carré de longueur 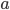puis on calculait son aire. Mais qu'est-ce que ça voulait dire un carré d'aire négative? Mes profs, tous autant théoriques les uns que les autres, essayaient vainement de nous dessiner des graphes au tableau noir. Vraiment pas très attirant. Encore pire s'ils utilisaient la craie rose. C'est alors que j'ai eu l'idée - ou plutôt l'idée m'a eu - de représenter ces nombres en deux dimensions avec deux dimensions de couleur. Le noir serait zéro, l'infini serait blanc, et on utiliserait les couleurs pour les autres nombres.... L'idée en tête - on est en 2003 -, je demande à mon grand frère s'il ne pourrait pas faire un programme pour cela. Il n'a pas le temps, et je le comprends, il est en train de passer ses concours. Arrivé en classes préparatoires quelques mois plus tard, en septembre 2003, j'ai découvert mon premier langage de programmation, Caml, qui contrairement à un paquet éponyme n'est normalement pas dangereux pour la santé, sauf s'il on en devenait accro au point d'y passer des nuits blanches. Heureusement, ce n'était pas trop mon cas. A l'époque, je dormais 8h30 par nuit et quelques soirées m'ont permit de développer mon premier prototype de traceur complexe. La première image que j'ai obtenue ressemblait à ça:

Des couleurs vives, un zéro noir, un infini blanc, c'est ce que je voulais! Entre cette version et la version actuelle, il y a très peu de différences. Maintenant les couleurs sont un peu moins vives et mieux réparties pour qu'on ait la propriété suivante: la reflex de 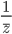est exactement celle de 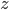mais en négatif,

Les premières fonctions non complexes

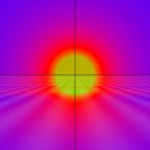
Une fois que ça marchait, je me suis mis avec frénésie à tester mes premières fonctions. Au fur et à mesure de mes trouvailles, je les montrais à ma famille qui observait le tout avec délectation! Ainsi, je leur ai montré un soleil couchant complexe. Pour la troisième image, j'ai retrouvé la formule, alors vous pouvez la retrouver et même la personnaliser sur reflex4you en cliquant dessus.

Si vous êtes matheux, vous vous rendrez compte que ces fonctions n'ont rien de "complexe" à part avoir deux variables. Mais peu importe, je me suis aperçu qu'avec des formules simples on pouvait obtenir de beaux résultats. Par exemple:

Les premières fonctions complexes

Je n'avais pas fait tout ce chemin pour des spirales multicolores.  Je me suis vite remis à l'analyse des fonctions complexes. Quand j'ai redécouvert les polynômes et les fractions rationnelles, ils n'étaient plus vraiment les même. Au lieu d'avoir des courbes de chameaux ou dromadaires, j'avais des points noirs aux milieux de symphonies multicolores.

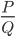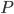J'ai tout de suite remarqué un théorème élémentaire: Pour une fraction , si est de degré 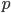et 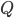de degré 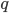, alors il y a 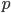points noirs et 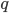points blancs ! Il s'agit du théorème de d'Alembert. Et ce n'est pas tout : Si 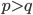,  alors la fonction devient blanche (c'est à dire que son module vers l'"infini") quand z s'éloigne de zéro. En revanche, si 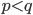, la fonction devient noire.

Les premières fractales

La vie est pleine de trucs. Il suffit d'avoir une nouvelle invention pour qu'on lui trouve des "trucs". Vous savez, le truc qui fait que d'un seul coup, ça prend une autre dimension. Un des premiers "trucs" que j'ai réalisé, c'est que si je composais plusieurs fois de telles fonctions par elles-mêmes, j'obtenais... des fractales ! Et des tonnes, pour pas cher !

La raison? Elle était simple. En fait, quand on trace une fonction complexe genre à quatre racines, ce qu'on fait en réalité c'est remplacer l'identité par la fonction.

Vous voyez la suite ?... Si on continue sur chacune des "petites identités", on répète le motif à l'infini. Pour peu que pour certaines valeurs on observe une convergence, on obtient de belles fractales que l'on peut modifier à souhait.

Captures d'écran d'époque

Revenons à nos moutons (colorés). Je ne voulais pas écrire un article mathématique, mais juste historique. Si vous voulez plus de détails, vous pouvez directement aller sur mon blog reflex. Continuons plutôt vers notre nouveau site www.reflex4you.com.

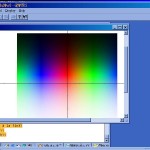
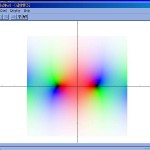
Lorsque j'ai commencé le développement, mon premier vrai langage de programmation était Caml, et j'avais donc accès aux primitives graphiques. Voici quelques captures d'écran qui me rappellent le bon vieux temps, où on voit même des tests de couleur qui n'ont pas marché (troisième image). Dans l'ordre, on a une exponentielle renversée, un cosinus, un polynôme qui a raté, une expônentielle, un polynôme du quatrième degré et un sinus.

Pour ceux qui aimeraient en savoir plus, voici le rapport du traceur Reflex et de ses premières applications assez complet écrit en 2007. Toutes les images ont été tracées à la main.

Le secret?

Ah oui il y avait un secret. Rapidement, j'ai codé un générateur de formules aléatoires assez particulier, dont je ne dévoilerai pas la recette ici. Pour simplifier, il créait des arbres et les remplissait avec des formules, des nombres complexes, des cosinus, des exponentielles, des polynômes, etc.
Et c'est de là que m'est venue l'idée de reflex4you.com. Si on parvenait à avoir une formule pour chaque lettre, on pourrait faire des prénoms en fonctions complexes ! Facile à dire... mais je ne m'y suis pas attardé à l'époque.

De Caml au C++ : PDA

Bien sûr, peu de personnes allaient pouvoir profiter de ce logiciel développé totalement en local et qui n'était pas accessible ailleurs. C'est pour cela que lorsque les PDA (Personnal Digital Assistant) sont arrivés dans notre famille, j'ai installé Microsoft Embedded Visual Tools et j'ai codé ma première application qui traçait sur l'écran des fonctions complexes. Avec le style et et tous les paramètres visuels - on pouvait zoomer-, c'est une version dont je n'étais pas peu fier.

Mais le PDA avait ses défauts: S'il n'avait plus de batterie, tout était reformaté. Question partage sur internet, il ne fallait même pas y penser. On était encore loin de l'Android tel qu'on le connait maintenant. C'était plutôt une calculatrice de poche. L'interface était difficile à mettre à jour, il fallait trouver mieux.

Du PDA à l'ordinateur de bureau

Même en Caml, ce n'était pas pratique en fin de compte. On voulait rapidement générer des fractales, on ne le pouvait pas. Il y avait toute une procédure longue à suivre : Ouvrir Caml, Ouvrir le fichier, taper la commande suivante, ouvrir les graphiques. Je ne vous dis pas pour enregistrer !

C'est pour cela que j'ai commencé à créer l'interface en Autoit3 avec leur éditeur d'interface très bien fait Koda. Là, non seulement je pouvais ajouter des boutons à gogo, ce dont je ne me suis pas privé, mais en plus j'ai pu mettre le bouton genre "J'ai de la chance" qui faisait en un clic une fractale. J'ai pu préparer des scripts pour pouvoir modifier la formule avec coloration syntaxique, une barre de chargement, des variables que l'on pouvait changer, un créateur de séquence d'images pour réaliser des vidéos... Une belle panoplie qui s'est avéré assez fructueuse.

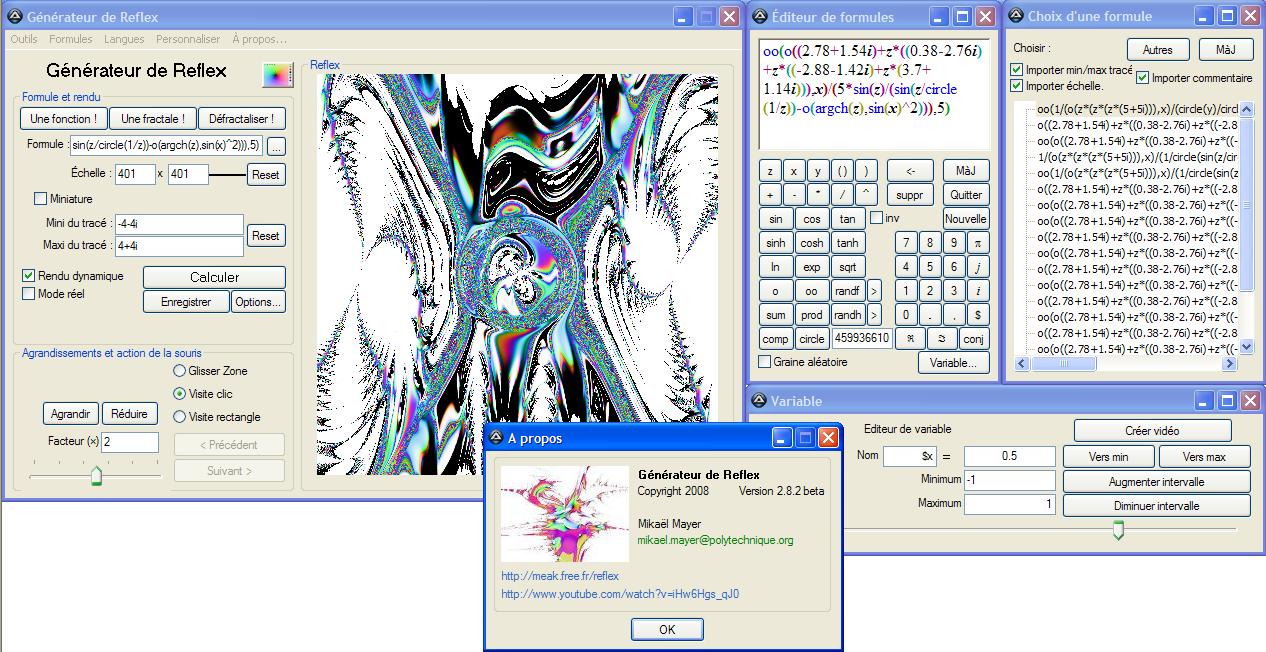
Mais personne n'y avait encore accès. Et pour cause: je n'avais pas mis cette version en ligne. Je peux toujours vous l'envoyez si vous voulez.

Un premier test: Internet

Avant de partir en mission, j'ai voulu mettre en ligne une version de traçage de Reflex.
Elle est encore en ligne
à l'heure actuelle mais pas très performante. Je ne voulais pas refaire toute une interface comme pour le PC. Déjà, ça m'avait pris beaucoup de temps pour mettre tous les fichiers en ligne, les compiler à distance sur le serveur bluehost, et les lier à un fichier php/html.

Le départ et le retour

Puis je suis parti en mission prêcher l'évangile, parce que dans la vraie vie, je suis chrétien - Saint des Derniers Jours - et c'est une chose pour laquelle je suis vraiment reconnaissant. Cela m'a arraché un peu à mon monde et m'a fait découvrir l'humain tel qu'il est, ses bons comme ses mauvais côtés et finalement l'harmonie du monde de la même manière que les fonctions complexes. C'était vraiment une expérience incroyable qui m'a beaucoup appris et m'a donné beaucoup d'optimisme et fortifié dans ma foi.

Je ferme la parenthèse, mais deux ans s'étaient écoulés, et je suis rentré en février 2012. L'idée de faire un site avec les fonctions complexes ne m'avait pas quitté. Au contraire, j'y voyais même encore plus clair qu'avant. Je ne voulais pas refaire un n-ième Mathematica/Maple/Wolfram Alpha en ligne où les gens pourraient taper leur formule et être content de l'image. Non, on pouvait faire BEAUCOUP mieux. Je m'y suis vaguement remis, mais j'avais d'autres choses en tête au début: Thèse, boulot, etc.

Réalisation finale

L'idée est apparue progressivement. Un prof de mathématiques à Montpellier aimait bien ces représentations de fonctions complexes et en faisait régulièrement part à ses élèves. Il m'a contacté, et vers septembre 2013 l'idée lui est venue de proposer à l'un de ses lycéens de m'aider dans un projet lié aux Reflex. Non seulement il en avait plusieurs d'intéressés, mais il m'a mis en contact avec l'un d'eux spécialement doué dans la programmation web. Je lui ai proposé quelques idées, et zou ! il avait déjà réalisé un site très rapidement. Le travail collaboratif que nous avons eu a été très fructueux puisqu'en moins de six mois à travailler sur le site, nous avons réussi à

• Recompiler Reflex Tracer depuis le C++ en ligne
• Ajouter autant de fonctions qu'il y a de lettres dans l'alphabet, et même plus
• Avoir une interface où en quelques clics on peut générer des formules personnalisées et les partager sur de multiples sites.
• Présenter une riche palette de filtres pour que la modification soient encore plus rapide et plus belle
• Trouver des moyens d'afficher la formule en LaTeX pour que les personnes se rendent compte qu'il s'agit de leur prénom.
• Connecter un magasin, en l'occurence zazzle,  pour permettre aux internautes de commander leur motifs préférés
• Et même, cerise sur le gâteau,  programmer un jeu 2048 en version complexe qui sert à passer le temps en attendant la commande.

C'était vraiment une aventure hors du commun.  J'espère que vous aurez autant de plaisir à découvrir le site que nous à l'avoir programmé.

C'est la fin de ce billet de blog. Si vous n'avez pas encore cliqué sur le lien pour accéder au site, le revoilà, et bonne visite !

http://www.reflex4you.com/